MuMath-Code

Link : https://arxiv.org/pdf/2405.07551v1

---

Notes

• Known current two methods of enhancing mathematical reasoning capability
  • Tool-use LLMs , integrate with external python interpreters
    • Code executors substantially supplant LLMs in particularly challenging computational and logical tasks, thereby alleviating the problem-solving burden on them.
  • Tool-free methods, augmenting math reasoning data.
    • The tool-free methods synthesize a large number of new math problems and corresponding solutions, taking the original training math QA pairs as the initial data seeds. Scaling law theoretically provides the basis for the ongoing improvement of LLMs’ performance by constantly incorporating new training data.
• This paper explores the great method to integrate the above research paths.
  • novel method that integrates tool usage with data augmentation to large amount of multi-perspective mathematical questions and solutions.
  • utilize proprietary LLMs to generate Python code while synthesizing new solutions to math problems, and then fine-tune the open-source models on the augmented dataset
• The resulting model, MuMath-Code, is thus equipped with the ability to write code for math problem solving.
• Chain of Thought (CoT) and Program of Though (PoT)
  • only CoT to solve
  • only PoT to solve
  • either CoT or PoT to solve depending on the solution
  • both CoT and PoT interleaves over multiple turns for the solution
• The dataset have a focus on greater diversity and exposing the model to a broader scope of novel questions, that significantly enhanced the model’s generalization capabilities.

Contributions of paper

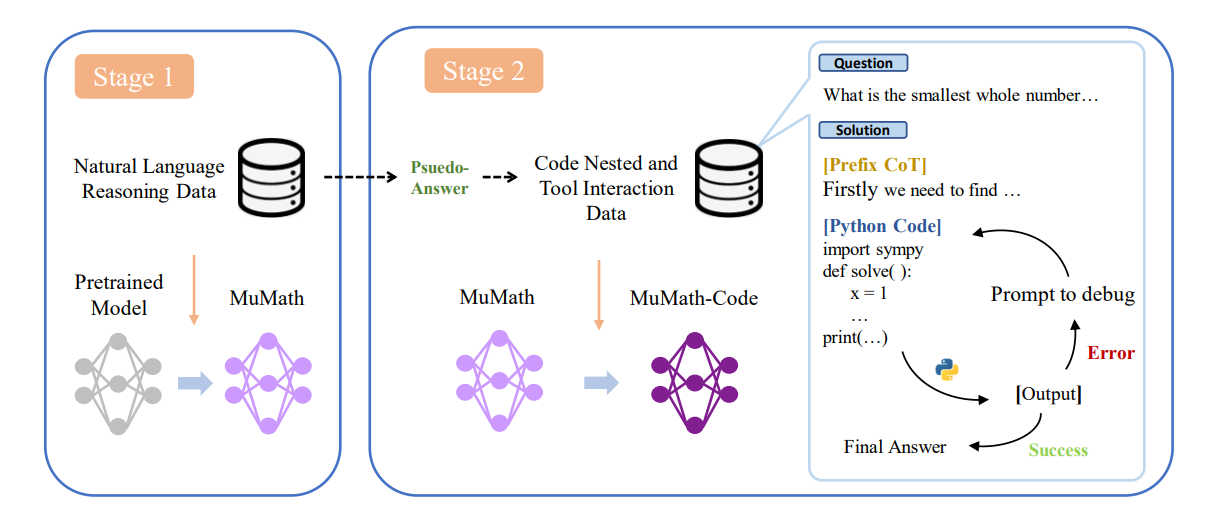
• Multi-perspective augmentation dataset with code-nested solutions for math problem solving, called MuMath-Code-Data.
• Design a two-stage training strategy to equip the open LLMs with pure language reasoning and math related code generation capabilities.
• state-of-the-art performance on GSM8K and MATH eval

MuMath Augmented Questions

Original questions from training set of GSM8K and MATH as seed questions. The augmenting methods are employed in MuMath are conducted on the seed set.

• Rephrasing: Rewrite a text while keeping the original meaning unchanged.
• Question Alteration: Alter the original questions, like changing numbers and adding more conditions, as in MuggleMath.
• FOBAR: Mask a certain condition in an initial question by substituting it with ‘X’, and meanwhile give the answer to the original question as a new condition, thereby creating a reverse question that seeks to determine the value of the unknown X
• BF-Trans: Backward-Forward Transformation. First utilize FOBAR transform question into a backward one, then rephase the question in a new form where the masked value is requested directly. Resulting in a ‘secondary forward’.

Generate two dataset MuMath-Data and MuMath-Code-Data for stage 1 and stage 2 respectively.

• MuMath-Data

  • 750K samples with pure CoT reasoning solutions to questions in Q

• MuMath-Code-Data

  • Code-nested solutions for the models to learn, each consisting of multi-turn code generation, code execution and pure natural language reasoning.
  • Similar to MathCoder and ToRA
  • In addition, the paper proposed prefix CoT, code debugging, and pseudo-answer guidance filtering.

---

Stage 1 training

• Finetune Llama on pure CoT data to get an intermediate model
• Models concentrate on learning the capability of pure CoT math reasoning.

Stage 2 training

• Finetune on code-nested data to get MuMath-Code-7b
• Models concentrate on PoT-CoT interleaved data to learn how to interact with an external tool (i.e., the Python interpreter).
• The loss of the outputs from the code execution is mask.